📌 백준 [9095]: 1, 2, 3 더하기
🔗 문제 링크
문제 설명 📄
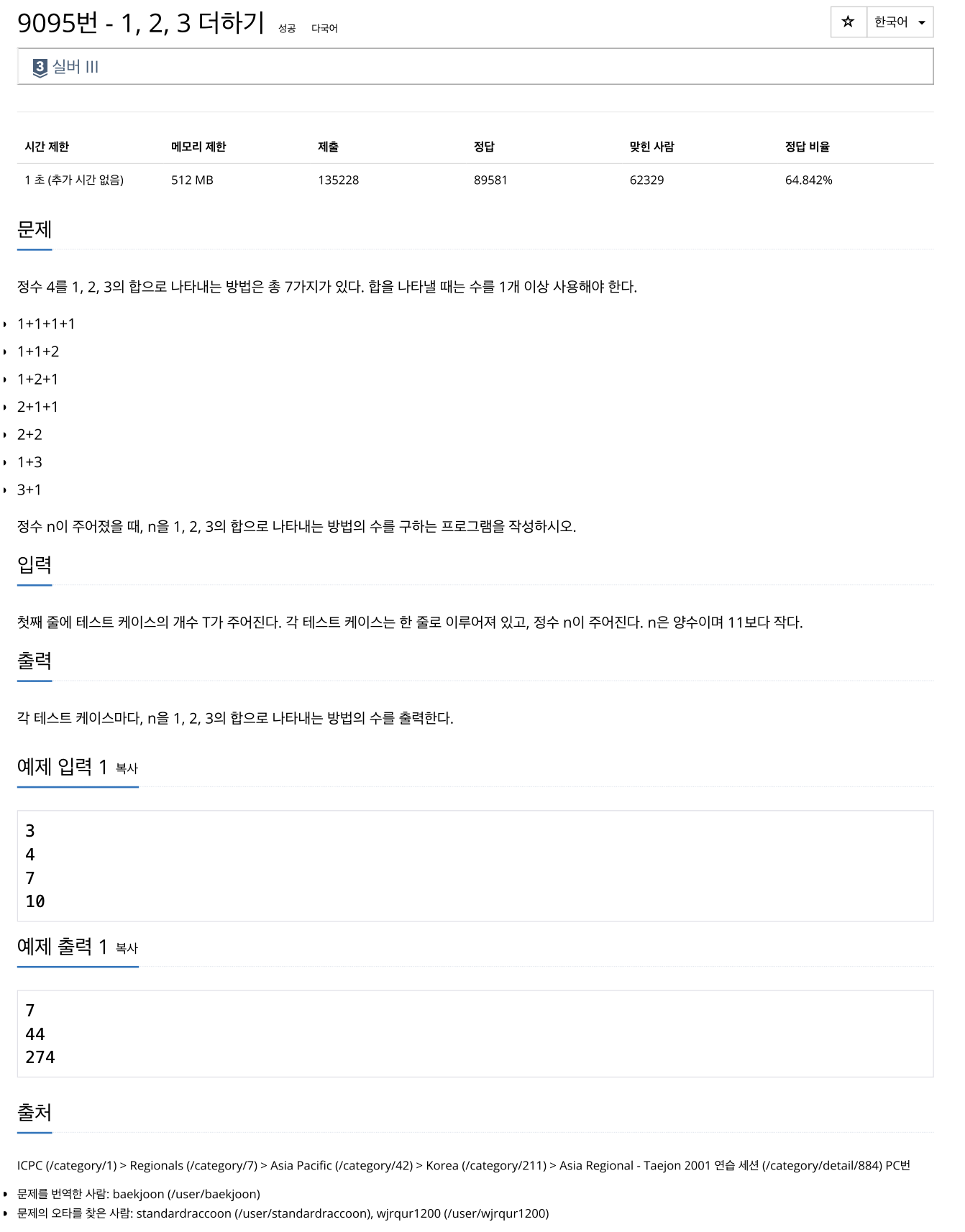
정수 n이 주어졌을 때, 1, 2, 3의 합으로 나타내는 방법의 수를 구하는 프로그램을 작성하시오.
예를 들어, n=4라면 1+1+1+1, 1+1+2, 1+2+1, 2+1+1, 2+2, 1+3, 3+1과 같이 7가지 방법이 있다.
문제 접근 방식 💡
- 재귀를 사용해 숫자를 1, 2, 3을 더해가며 n에 도달하는 모든 경우의 수를 계산.
- 주어진 숫자를 초과하는 경우 탐색을 종료.
- 최적화를 위해 재귀를 반복적으로 호출.
Solution 💻
count = int(input())
def func(num):
global answer
global target
if num == target:
answer += 1
return
if num > target:
return
func(num + 1)
func(num + 2)
func(num + 3)
for _ in range(count):
answer = 0
target = int(input())
func(0)
print(answer)
시간 복잡도 분석 ⏲️
- 시간 복잡도: O(3^n)
- 재귀 호출에서 각 단계마다 최대 3번의 분기 발생.
공간 복잡도 분석 🗄️
- 공간 복잡도: O(n)
- 재귀 호출 스택의 최대 깊이는 n에 비례.
리팩토링 🛠️
def count_ways(n):
dp = [0] * (n + 1)
dp[0] = 1
for i in range(1, n + 1):
if i >= 1:
dp[i] += dp[i - 1]
if i >= 2:
dp[i] += dp[i - 2]
if i >= 3:
dp[i] += dp[i - 3]
return dp[n]
count = int(input())
for _ in range(count):
target = int(input())
print(count_ways(target))
시간 복잡도 분석 ⏲️
- 시간 복잡도: O(n)
- 동적 프로그래밍으로 각 숫자에 대해 최대 3번의 연산만 수행.
공간 복잡도 분석 🗄️
- 공간 복잡도: O(n)
- DP 배열에 n+1개의 공간 사용.
'알고리즘 > 백준' 카테고리의 다른 글
| 백준 [11048]: 이동하기 (1) | 2025.01.14 |
|---|---|
| 백준 [11726]: 2×n 타일링 (0) | 2025.01.14 |
| 백준 [11057]: 오르막 수 (1) | 2025.01.14 |
| 백준 [11727]: 2×n 타일링 2 (1) | 2025.01.13 |
| 백준 [2579]: 계단 오르기 (0) | 2025.01.12 |
