📌 백준 [11048]: 이동하기
🔗 문제 링크
문제 설명 📄
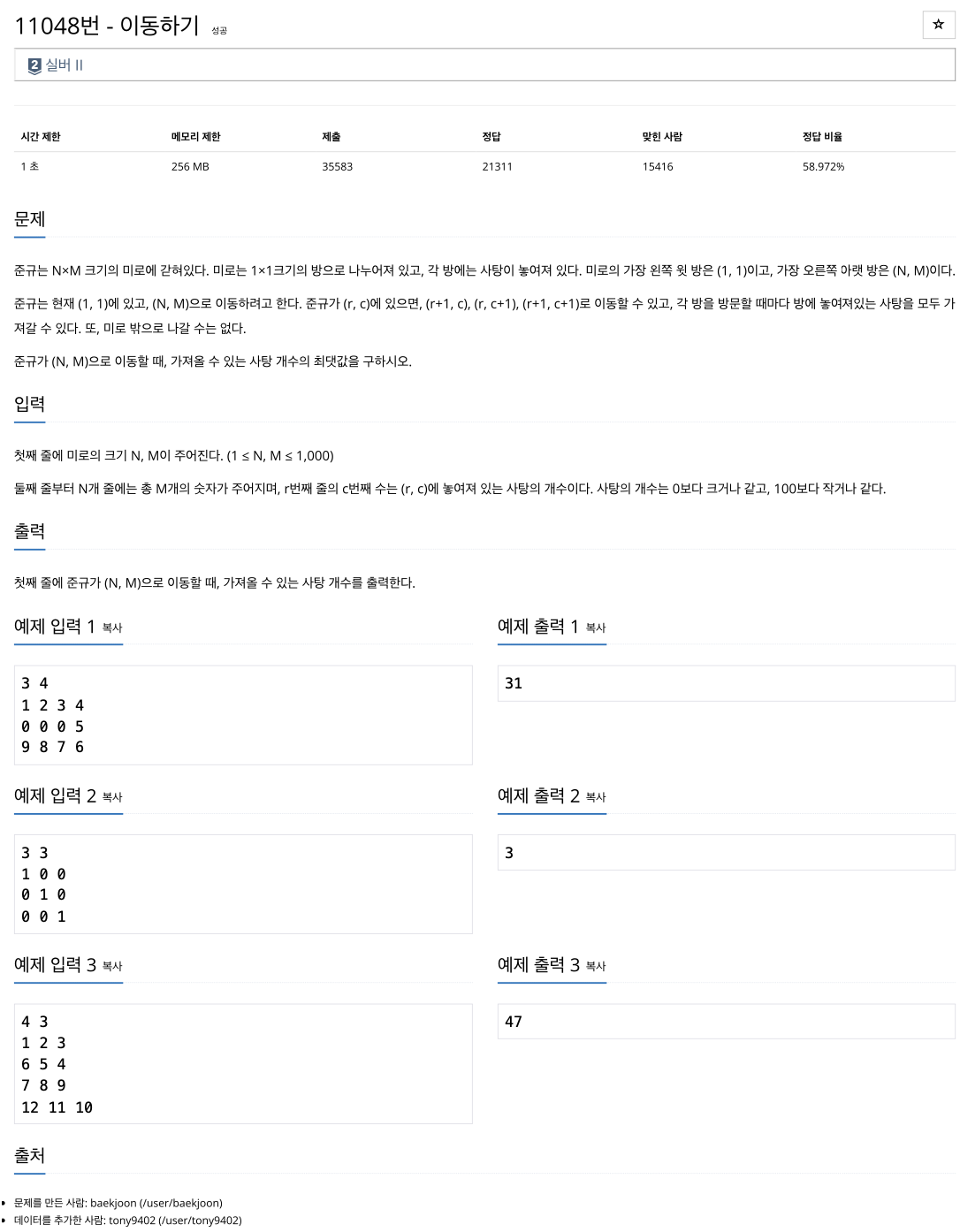
N×M 크기의 미로가 주어진다. 각각의 칸에는 아이템의 개수가 적혀 있다.
왼쪽 위에서 시작하여 오른쪽 아래까지 이동하려고 한다.
이때, 한 번에 오른쪽, 아래쪽, 또는 대각선 아래로만 이동할 수 있다.
아이템을 최대한 많이 줍기 위해 가져올 수 있는 아이템의 최대 개수를 구하시오.
문제 접근 방식 💡
- 동적 프로그래밍(DP) 배열 dp[i][j]를 사용하여 (i, j)까지 이동했을 때의 최대 아이템 개수를 저장.
- 초기값: dp[0][0] = miro[0][0].
- 점화식:
- dp[i][j] = max(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + miro[i][j] (단, 경계를 벗어나지 않도록 조건 추가).
Solution 💻
n, m = map(int, input().split())
miro = [[int(i) for i in input().split()] for _ in range(n)]
dp = [[0 for _ in range(m)] for _ in range(n)]
dp[0][0] = miro[0][0]
for r in range(n):
for c in range(m):
if r > 0:
dp[r][c] = max(dp[r][c], dp[r - 1][c] + miro[r][c])
if c > 0:
dp[r][c] = max(dp[r][c], dp[r][c - 1] + miro[r][c])
if r > 0 and c > 0:
dp[r][c] = max(dp[r][c], dp[r - 1][c - 1] + miro[r][c])
print(dp[n - 1][m - 1])
시간 복잡도 분석 ⏲️
- 시간 복잡도: O(n × m)
- 이중 반복문을 사용하여 DP 테이블을 채움.
공간 복잡도 분석 🗄️
- 공간 복잡도: O(n × m)
- DP 테이블과 미로 배열의 크기가 n × m.
리팩토링 🛠️
n, m = map(int, input().split())
miro = [[int(i) for i in input().split()] for _ in range(n)]
dp = [[0] * m for _ in range(n)]
for r in range(n):
for c in range(m):
dp[r][c] = miro[r][c]
if r > 0:
dp[r][c] = max(dp[r][c], dp[r - 1][c] + miro[r][c])
if c > 0:
dp[r][c] = max(dp[r][c], dp[r][c - 1] + miro[r][c])
if r > 0 and c > 0:
dp[r][c] = max(dp[r][c], dp[r - 1][c - 1] + miro[r][c])
print(dp[-1][-1])
시간 복잡도 분석 ⏲️
- 시간 복잡도: O(n × m)
- 이중 반복문을 통해 DP 테이블을 계산.
공간 복잡도 분석 🗄️
- 공간 복잡도: O(n × m)
- DP 테이블과 미로 배열의 크기가 n × m.
'알고리즘 > 백준' 카테고리의 다른 글
| 백준 [10844]: 쉬운 계단 수 (0) | 2025.01.18 |
|---|---|
| 백준 [1699]: 제곱수의 합 (1) | 2025.01.16 |
| 백준 [11726]: 2×n 타일링 (0) | 2025.01.14 |
| 백준 [11057]: 오르막 수 (1) | 2025.01.14 |
| 백준 [11727]: 2×n 타일링 2 (1) | 2025.01.13 |
