📌 LeetCode [39]: Combination Sum
🔗 문제 링크
문제 설명 📄
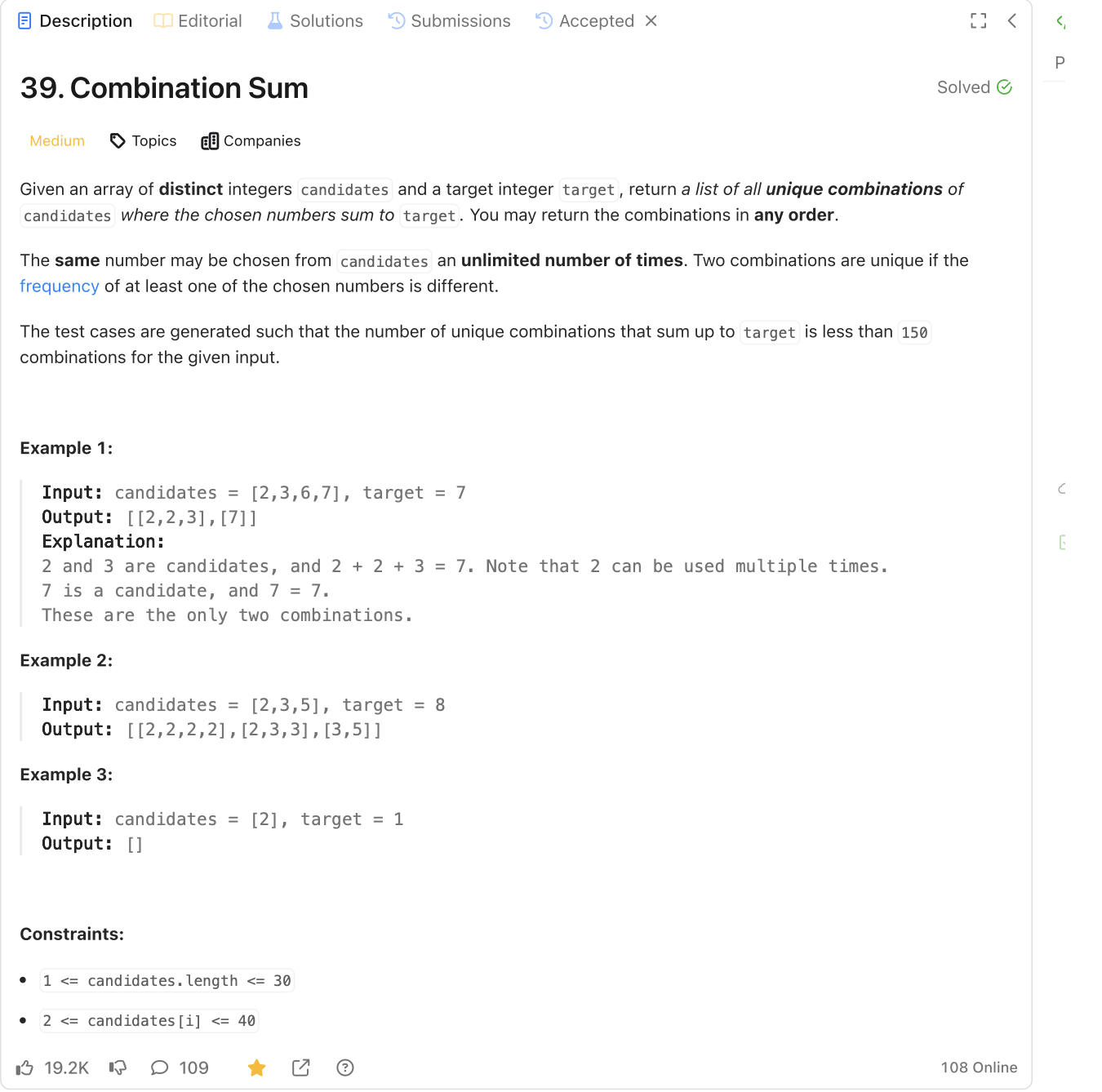
정수 배열
candidates와 정수target이 주어질 때, 후보 숫자들로부터 조합하여 합이target이 되는 모든 고유한 조합을 반환하는 문제입니다.
각 숫자는 무한히 재사용될 수 있으며, 반환된 조합은 사전 순으로 정렬되어야 합니다.
문제 접근 방식 📋
문제는 백트래킹(Backtracking) 기법을 사용하여 해결할 수 있습니다. 숫자들이 중복되지 않고, 무한히 재사용 가능하므로 각 후보 숫자를 여러 번 포함할 수 있습니다.
아이디어 설명 💡
- 정렬: 먼저
candidates배열을 정렬합니다. 이를 통해 더 이상target에 도달할 가능성이 없는 경우 반복을 조기에 종료할 수 있습니다. - 백트래킹:
- 현재 조합(
current)과 시작 인덱스(start), 남은 목표값(target)을 재귀적으로 추적합니다. - 목표값(
target)이 0이면 현재 조합을 결과 리스트에 추가합니다. - 목표값이 음수가 되면, 백트래킹하여 재귀를 종료합니다.
- 현재 조합(
- 가지치기: 이미
candidates를 정렬했으므로, 목표값(target)에서 후보 숫자를 뺀 결과가 음수가 되면 반복문을 종료할 수 있습니다.
Solution 💻
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
def backtrack(current, start, target):
if target == 0:
result.append(list(current))
return
if target < 0:
return
for i in range(start, len(candidates)):
if target - candidates[i] < 0:
return
current.append(candidates[i])
backtrack(current, i, target - candidates[i])
current.pop()
result = []
candidates.sort()
backtrack([], 0, target)
return result시간 복잡도 분석 ⏲️
- 시간 복잡도:
O(2^n)- 각 숫자를 무한히 선택할 수 있으므로, 가능한 조합의 수가 지수적으로 증가합니다.
- 공간 복잡도:
O(target / min(candidates))- 재귀 호출 스택의 깊이는 목표값(
target)과 가장 작은 숫자의 비율에 비례합니다.
- 재귀 호출 스택의 깊이는 목표값(
리팩토링 🛠️
개선된 코드
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
def backtrack(current, start, target):
if target == 0:
result.append(current[:])
return
for i in range(start, len(candidates)):
if candidates[i] > target:
break
current.append(candidates[i])
backtrack(current, i, target - candidates[i])
current.pop()
result = []
candidates.sort()
backtrack([], 0, target)
return result개선된 코드의 차이점
- 백트래킹 대신 동적 계획법(DP)을 사용하여 문제를 해결했습니다.
dp[i]를 정의하여 숫자i를 만들기 위한 모든 조합을 저장했습니다.- 각 후보 숫자를 순회하며, 가능한 조합을 점진적으로 추가했습니다.
시간 복잡도 분석 ⏲️
- 시간 복잡도:
O(target * len(candidates) * avg_combinations) - 공간 복잡도:
O(target * avg_combinations)
'알고리즘 > 리트코드' 카테고리의 다른 글
| LeetCode [268]: Missing Number (0) | 2024.11.21 |
|---|---|
| LeetCode [125]: Valid Palindrome (2) | 2024.11.21 |
| LeetCode [238]: Product of Array Except Self (1) | 2024.11.20 |
| LeetCode [1]: Two Sum (0) | 2024.11.19 |
| LeetCode [338]: Counting Bits (0) | 2024.11.18 |
