📌 LeetCode [1603]: Design Parking System
🔗 문제 링크
문제 설명 📄
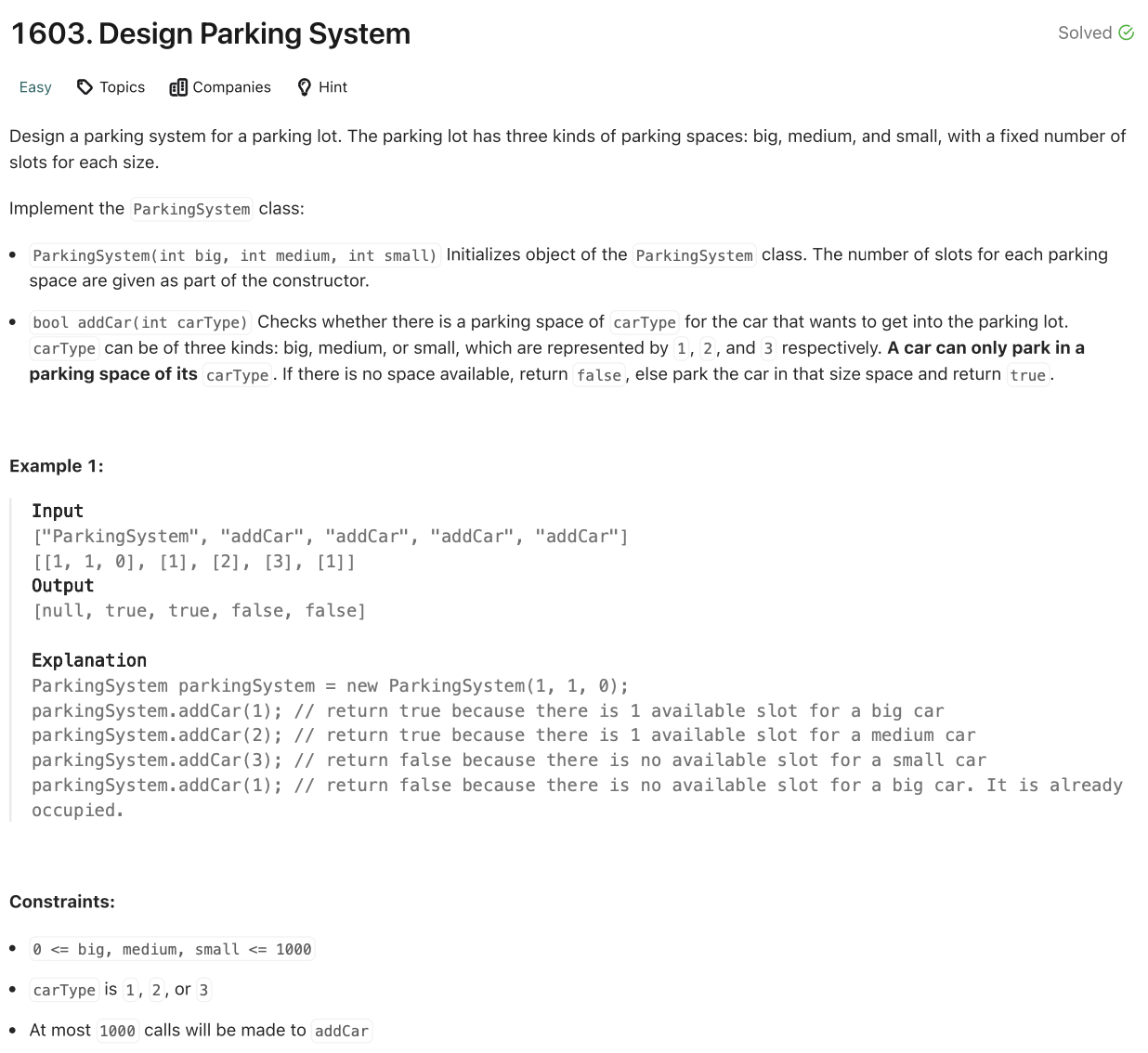
주어진 주차 공간 크기에 따라 주차가 가능한지 확인하고, 성공적으로 주차한 경우 해당 공간의 카운트를 줄이는 프로그램을 작성하세요.
ParkingSystem클래스는 세 가지 유형의 주차 공간을 관리합니다:big: 대형차를 위한 공간medium: 중형차를 위한 공간small: 소형차를 위한 공간
addCar(carType: int) -> bool메서드는 차량의 유형을 입력받아, 주차가 가능하면True를 반환하고 공간을 1 줄입니다. 공간이 부족하면False를 반환합니다.
문제 해결 접근 ✨
- 공간 초기화:
- 생성자를 통해 대형, 중형, 소형 공간의 초기 개수를 저장합니다.
- 차량 유형에 따른 주차 가능 여부 확인:
- 입력된 차량 유형에 따라 공간을 확인하고, 가능하면 공간을 줄이며
True를 반환합니다. - 공간이 부족하면
False를 반환합니다.
- 입력된 차량 유형에 따라 공간을 확인하고, 가능하면 공간을 줄이며
- 효율성:
- 조건문을 통해 간단히 구현하여 (O(1))의 시간 복잡도를 가집니다.
Solution 💻
class ParkingSystem:
def __init__(self, big: int, medium: int, small: int):
self.bigCar = big
self.mediumCar = medium
self.smallCar = small
def addCar(self, carType: int) -> bool:
if carType == 1:
if self.bigCar > 0:
self.bigCar -= 1
return True
elif carType == 2:
if self.mediumCar > 0:
self.mediumCar -= 1
return True
else:
if self.smallCar > 0:
self.smallCar -= 1
return True
return False
# Your ParkingSystem object will be instantiated and called as such:
# obj = ParkingSystem(big, medium, small)
# param_1 = obj.addCar(carType)시간 복잡도 분석 ⏲️
- 공간 초기화: 생성자는 (O(1)).
addCar메서드: 차량 유형에 따라 조건문을 통해 주차 가능 여부를 확인하므로 (O(1)).- 총 시간 복잡도: (O(1)).
공간 복잡도 분석 🗄️
- 필요한 공간: 각 주차 공간의 상태를 저장하는 세 개의 정수 값으로 (O(1)).
- 총 공간 복잡도: (O(1)).
'알고리즘 > 리트코드' 카테고리의 다른 글
| LeetCode [2900]: Longest Unequal Adjacent Groups Subsequence I (2) | 2024.12.30 |
|---|---|
| LeetCode [824]: Goat Latin (0) | 2024.12.29 |
| LeetCode [1046]: Last Stone Weight (0) | 2024.12.27 |
| LeetCode [496]: Next Greater Element I (1) | 2024.12.26 |
| LeetCode [258]: Add Digits (1) | 2024.12.25 |
